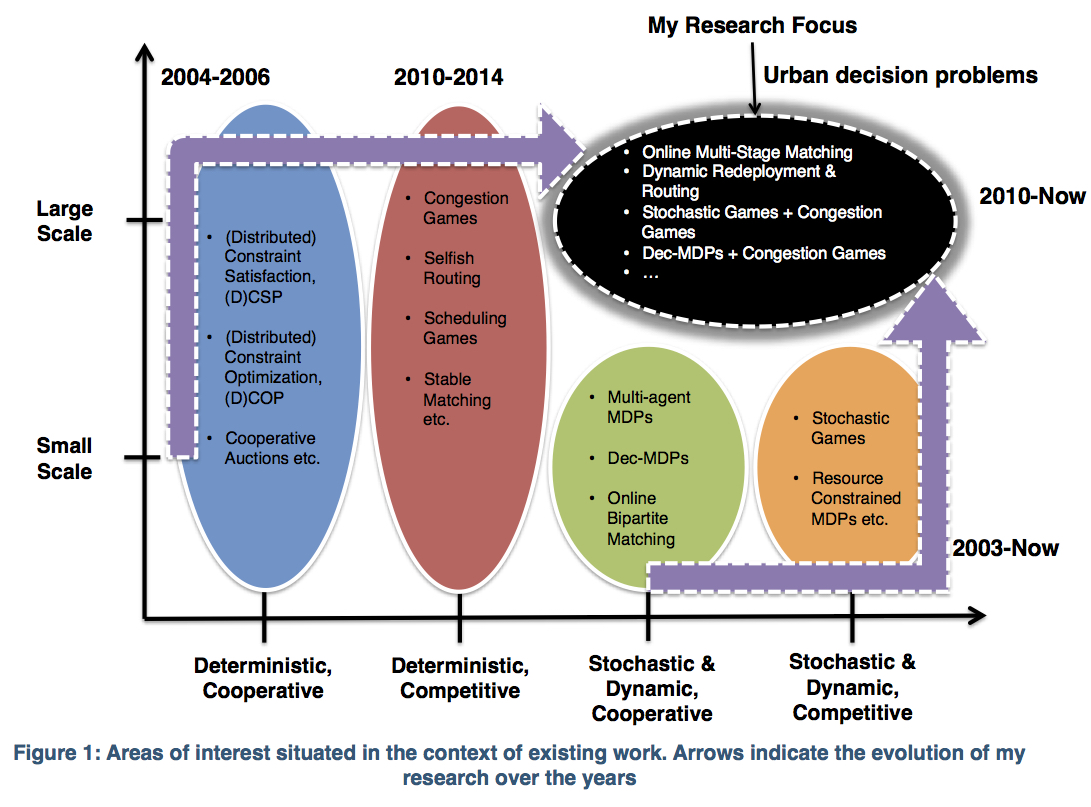
Rapid "urbanization" - more than 50% of world's population now resides in cities - coupled with the natural lack of coordination in usage of common resources (ex: landmarks, malls, bikes, ambulances, taxis, security personnel) has deteriorated a wide variety of quality of life metrics such as waiting times in queues, response time for emergency needs, number of traffic accidents/ violations in cities of today. Thus, my long term goal is to build intelligent agent systems (single and multi-agent cooperative/competitive systems) that make sequential (connected) set of decisions to continually match supply of resources to the unpredictable demand for resources in urban environments to optimize quality of life metrics. My aim is to achieve this matching through a combination of computational and behavioural methods rooted in Artificial Intelligence and Machine Learning, Operations Research and Behavioural Economics.
Many decision problems in urban environments can be characterised as requiring a match between limited resource supply and an unpredictable demand for resources. Given below are a few practical real world urban decision problems that motivate my research:
- Taxi fleets: Resource supply corresponds to the available taxis and demand corresponds to customers needing taxis. The goal in this problem is to increase revenues for taxis (or reduce wait times for customers) by continuously matching available taxis to customer demand or proxies for customer demand (ex: taxi stands).
- Emergency Response: Resource supply corresponds to ambulances or fire trucks at base stations and demand corresponds to emergency events. The goal in this problem is to reduce response time for emergency events by dynamically moving the "right" ambulances to the "right" base stations.
- Traffic and Security Patrols: Resource supply corresponds to traffic or security personnel and demand corresponds to potential for traffic violations or security incidents at different nodes in a network. The goal in this problem is to prevent traffic violations and security incidents by reducing predictability in patrols of traffic/security personnel in the network without sacrificing on coverage of "important" locations.
- Bike sharing systems: Resource supply corresponds to available bikes at base stations and demand corresponds to customers needing bikes. The goal in this problem is to reduce lost demand due to unavailability of bikes at base stations. We are focussed on lost demand, as it can lead to customers employing private vehicles, which in turn will lead to increased carbon
We have developed models and approaches that lie at the intersection of Artificial Intelligence, Operations Research, Game Theory and Behavioural Economics to solve scalability issues for these dynamic matching problems. Our solution methods for these urban decision problems are based on exploiting basic properties of the urban environments and have been evaluated on real world data sets:
- Exploiting Homogeneity and Anonymity: Typically in urban environments, there is homogeneity in supply (ex: 90\% of taxis in Singapore are identical and have same fare structure) and demand components (ex: customers going from a source to a destination are identical from the perspective of taxis) and more over there is anonymity in interactions between supply and demand (ex: assigning any one of the two taxis at a taxi stand to a near by customer typically have identical match value).
- Exploiting Limited Influence of Individual Entities (Supply/Demand): While there are typically a large number of entities involved in urban environments, the impact of each of them on the overall outcome is typically very small.
- Exploiting abstraction: Urban decision problems where there is supply demand matching are amenable to abstraction. That is to say, we initially abstract a group of supply components (depending on specific domain properties) into an abstract supply component and create an abstract problem. The sequential decision strategy to match supply and demand can initially be computed for this abstracted problem and then incrementally improved by reducing the abstraction in the problem. We have successfully demonstrated this in the context of bike sharing systems.
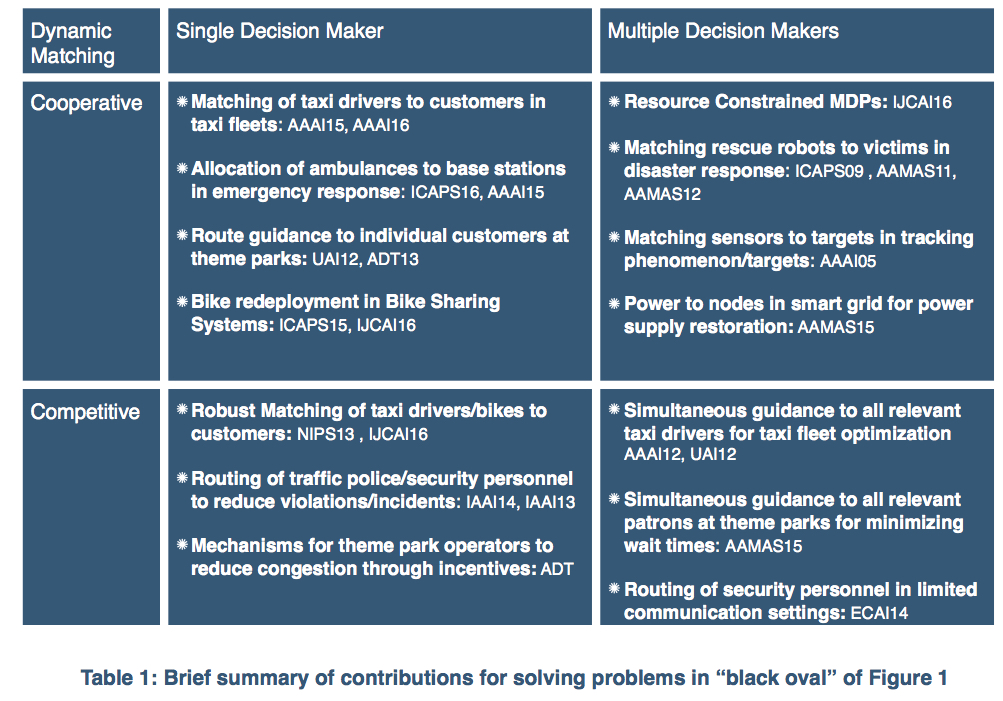
- Exploiting decomposability: In many of the urban decision problems, it is easy to identify multiple parts of the overall problem that are nearly decomposable. For instance, in bike sharing systems, the problem of moving bikes between stations so as to reduce lost demand and the problem of finding routes for trucks that move bikes are nearly decomposable. Table 1 provides a brief summary of our contributions characterised according to the application.